Atomic Nuclei and Pairing Correlations

This work was done by LaGuardia students Josselyn Velasquez and Bai Huang as a part of the Honors “General Physics I” class, Fall 2018. The project investigates the effects of pairing correlations in atomic nuclei.

The project was conducted under the supervision of Dr. Roman Senkov.

Other research projects done by students in the Physics Honors courses: “Orbital Decay of a Massive Black Hole” and “Computer Modelling of Physical Systems”.

Download this article: pdf (734Kb)


Abstract

In this research we studied the effects of the pairing correlations in atomic nuclei. We analyzed the existing experimental data, namely the neutron and proton separation energies, for about 40 nuclei in sd-shell and could (1) see the manifestations of the nuclear single-particle levels and the effects of the pairing correlations between nucleons and (2) build a simple model which can explain the experimental data. We estimated the first single-particle energy level in the sd-shell and extracted the pairing correlation energies \(\Delta_{p,n}\) for these nuclei. As the result we concluded that the first level in the sd-shell has the total angular momentum j=5/2 and the energy \(\epsilon \approx 4+2(A-16)\), where the energy is in MeV and A is the mass number. For the pairing correlation energies we got \(\Delta_p \approx 4.5\) MeV and \(\Delta_n \approx 4\) MeV.

1. Introduction

Most of the matter we see around is made of atoms, which are the building blocks of everything and are very small in size. Every atom consists of a heavy nucleus at the center and the electrons orbiting around. The nucleus is about 2,000 times heavier than the electrons and 100,000 times smaller than the atom. Thus nuclei are extremely small, but carry 99.95% of the atomic mass. Each nucleus consists of two kinds of particles: protons and neutrons, so it is enough to provide the number of protons and neutrons to completely identify the nucleus. For example, a nuclear system with 8 protons (Z=8) and 8 neutrons (N=8) is a nucleus of oxygen-16. Protons and neutrons have very similar properties with respect to the nuclear forces, for example, protons and neutrons have almost equal masses. This similarity allows us to call them nucleons and is reflected in, so called, isospin symmetry of the nuclear forces. The isospin symmetry is violated by the electro-magnetic interaction since protons are positively charged particles and neutrons have no electric charge (they are neutral).

It is very important to have a better understanding of the nuclear forces and nuclear structure because it can help us to advance in many areas of human interests such as nuclear power (construct more safe and efficient nuclear reactors), nuclear medicine (where small amounts of radioactive particles are used to obtain information about our bodies), nuclear astrophysics (explain the nuclear synthesis and evolution of stars), and so on. Nuclear physics is a challenging and interesting area of scientific research, nuclear systems are very complicated and hard to study. Majority of the modern nuclear theoretical researches demand serious computational efforts.

There are some consistent patterns in nuclear systems which help scientists to advance in studying of atomic nuclei quite significantly. In this project we investigated one of these phenomena, namely the nuclear pairing correlations. To “see” these correlations, we analyzed the existing experimental data on the nucleon separation energies for about 40 isotopes heavier than 16O but lighter than 40Ca. Separation energy is the minimum energy required to completely extract a nucleon from the nucleus, it can be measured relatively easily and the corresponding experimental data is available at the National Nuclear Data Center [1].

Table 1: The proton separation energies for N=14 isotones.
Element Symbol # protons # neutrons # nucleons Sp [MeV]
Nitrogen N 7 14 21 19.6
Oxygen O 8 14 22 23.26
Fluorine F 9 14 23 13.26
Neon Ne 10 14 24 16.55
Sodium Na 11 14 25 10.69
Magnesium Mg 12 14 26 14.14
Aluminum Al 13 14 27 8.27
Silicon Si 14 14 28 11.58
Phosphorus P 15 14 29 2.75
Sulfur S 16 14 30 4.4

Table 1 presents the experimental values for the proton separation energies (the last column) for N=14 isotones. Isotones are the nuclei which have the same number of neutrons, here N=14, but different number of protons, here from Z=7 to Z=16. The units used for the proton separation energies are MeV (Mega electron-Volts), which are typical for nuclear systems: 1 MeV = 106 eV = \(1.6\times 10^{-13}\) Joules. Figure 1 represents the same separation energies as Table 1 but graphically. We can notice a quite prominent odd-even effect, when the nuclei with odd and even number of protons have different separation energies: it seems that it is much harder to remove a nucleon from nuclei with even number of particles compared to the systems with odd number of particles.

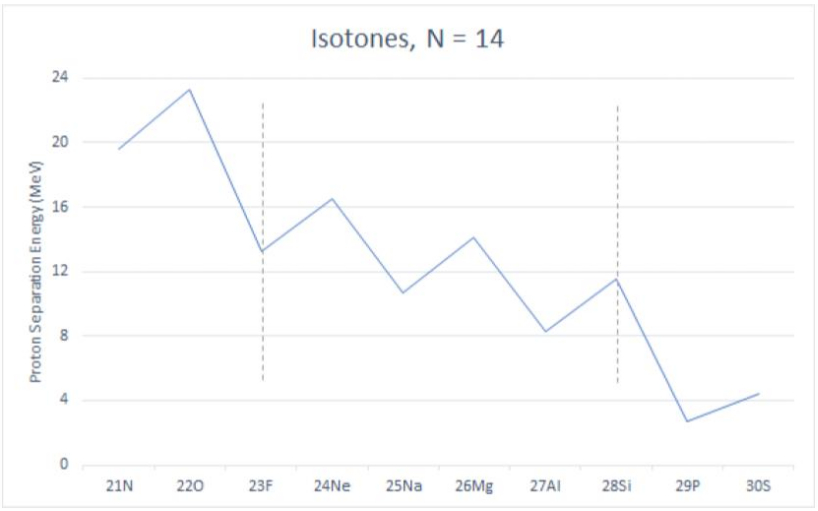
Figure 1. The proton separation energies (in MeV) are plotted for different isotones with 14 neutrons.

Such a zigzag change in the nucleon separation energy is not specific to the N=14 isotones, on the contrary, it is quite common and can be seen in practically any isotone and isotope chains. Another example is presented in Fig. 2, where the experimental neutron separation energies are plotted for a set of oxygen isotopes (isotopes are the systems with the same number of protons, but different number of neutrons), for more example also see Fig. 3. In the following section we will construct a theoretical model explaining this phenomenon and extract the corresponding parameters.

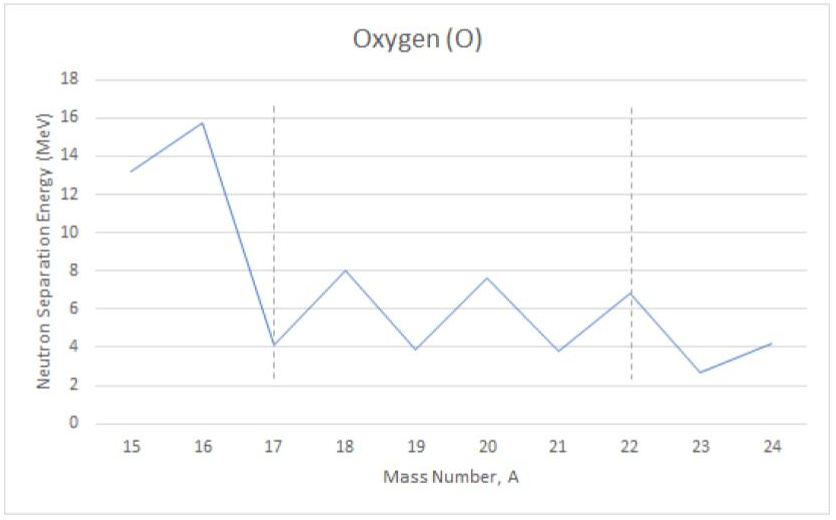
Figure 2. The neutron separation energies (in MeV) are plotted for different oxygen isotopes (Z=8) as a function of the total number of nucleons.

2. Pairing Correlations and Shell Structure

2.1 Experimental data

By analyzing the separation energies for N=14 isotones and Z=8 isotopes, there are several observations to be made:

  • There is a strong difference in the separation energies for the nuclei with an even number of neutrons or protons and nuclei with an odd number of particles. We can see that nuclear systems with even numbers of particles have higher separation energies, by about 4 MeV. This can be seen in both figures.
  • The neutron separation energy drops significantly after 16O (from 16 MeV to 4 MeV) in Fig. 2. We can notice a similar drop in the proton separation energy in Fig. 1 after 22O.
  • There is another relatively small drop in the separation energies after 22O (Fig. 2) and after 28Si (Fig. 1).
  • There are exactly 6 isotopes/isotones in between these two drops.

2.2 Theoretical model

Below we will construct a simple model which can explain the observations we noticed above. Let us accept the following postulates:

  • We can see that 8 protons and 8 neutrons are tightly bound by the nuclear forces, they form a nucleus of 16O, which can be considered as a rigid core with high separation energies, both for protons and neutrons. If we try to extract one of these nucleons we have to apply a relatively large energy. For example, 22O has {8 protons} and 14 neutrons and it's proton separation energy is high, see Fig. 1. Another example would be 16O, see Fig. 2.
  • The drop in the separation energies (see the left dashed lines in Figs. 1 and 2), once we add new particles and go beyond of 8 protons or 8 neutrons, can be explained by suggesting that these new particles occupy higher energy levels which are above the 16O core. These extra particles are less bound and are easier to extract from the nucleus. Thus we assume a certain energy level structure for nuclear systems close to oxygen-16, it is similar to atomic shell structure for electrons.
  • The second drop in the separation energies (see the right dashed lines in Figs. 1 and 2) can be explained by suggesting that the closest to the 16O core energy level is completely occupied and we begin to fill the next energy level, which is even higher in energy. Thus we established the existence of a nuclear single-particle level just above the oxygen core. The maximum number of identical particles (fermions) one can put on a quantum energy level defines its total angular momentum: Nmax=2j+1, where j is the total angular momentum of this level. If we take Nmax=6 then j=5/2.
  • Odd-even effect can be explained by introducing the pairing correlation energy. When we have two identical particles close to each other (like two protons or two neutrons on the same level) they tend to form a pair and the energy of the system decreases by the binding energy of this pair. In order to remove a nucleon from an even system we first have to break a pair and then remove the particle. For an odd system at least one particle is unpaired, so it will be easier to remove this particle from the nucleus because we do not have to break any pairs. This can explain the odd-even effect we have observed in Figs. 1, 2 and 3.
  • We suggest a simple schematic model describing energy of isotopes and isotones near 16O core. By adding new nucleons on top of the core, we occupy the next single-particle energy level so the energy of the system (relative to the core) can be written as \begin{equation} E=\epsilon N - \Delta N_p, \end{equation} where N is the number of nucleons above the core, \(\epsilon\) is the energy of this level (so called single-particle energy), \(\Delta\) is the pairing correlation energy, and \(N_p\) is the number of pairs on the level. For example, for 17O: N=1 and Np=0, for 18O: N=2 and Np=1, for 19O: N=3 and Np=1, and so on. If we are given \(\epsilon\) and \(\Delta\) parameters then we can calculate the nuclear separation energies for all isotopes near the oxygen core and compare them to the experimental values.
  • By fitting the experimental data presented on Figs. 1, 2, and 3 we can extract the parameters of our model described by Eq.(1). We found the single-particle energy is \(\epsilon \approx 4+2(A-16)\), where energy is in MeV and A is the total number of nucleons. For the pairing correlation energies we got \(\Delta_p \approx 4.5\) MeV and \(\Delta_n \approx 4\) MeV.

2.3 More Evidence Supporting our Model

Figure 3 exhibits similar qualities as observed for Oxygen isotopes and N=14 isotones. The odd-even effect is still present. Similar to the drop in separation energy observed in Oxygen, we observe drops here. Notably after 24Mg for Magnesium and after 28Si for Silicon.

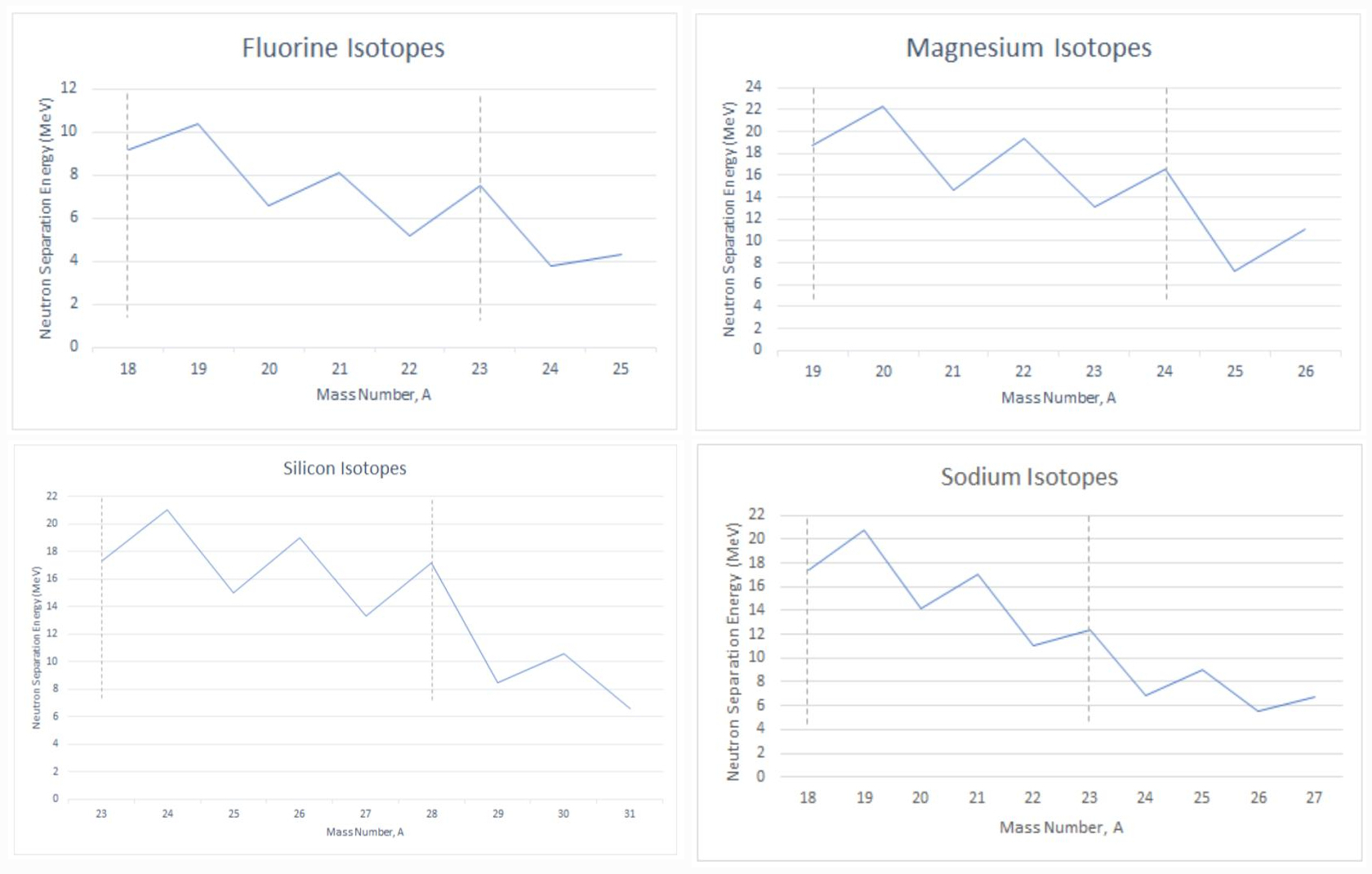
Figure 3. Neutron separation energies for four different isotopes. We can clearly see the effects of the nuclear pairing correlations and shell structure.

Results and Conclusion

By analyzing separation energies we have found a few correlations which are useful for studying underlying nuclear structure. We have observed a pairing correlation that corresponds to higher separation energy in nuclei where the number of nucleons is even. This suggests the existence of a pairing structure within the nucleus.

We have also found a drop in overall separation energy at specific thresholds for different isotopes, which exposes further nuclear structure. We can correlate these thresholds with the nuclear level structure of isotopes of each element. The most clear examples are the thresholds for Magnesium at 24Mg and Silicon at 28Si which correspond to the filling of certain single-particle energy levels for each element. We created a simple schematic model describing the energy of isotopes near oxygen-16 and defined it's parameter.

The authors would like to thank Dr. Roman Senkov for his help and guidance in this research project. The research was done as a part of the Honors General Physics I course at LaGuardia Community College.


References

[1] National Nuclear Data Center - Brookhaven National Laboratory, https://www.nndc.bnl.gov/